3-工厂模式 - 创建型模式
本文共 2118 字,大约阅读时间需要 7 分钟。
文章目录
1. 例子
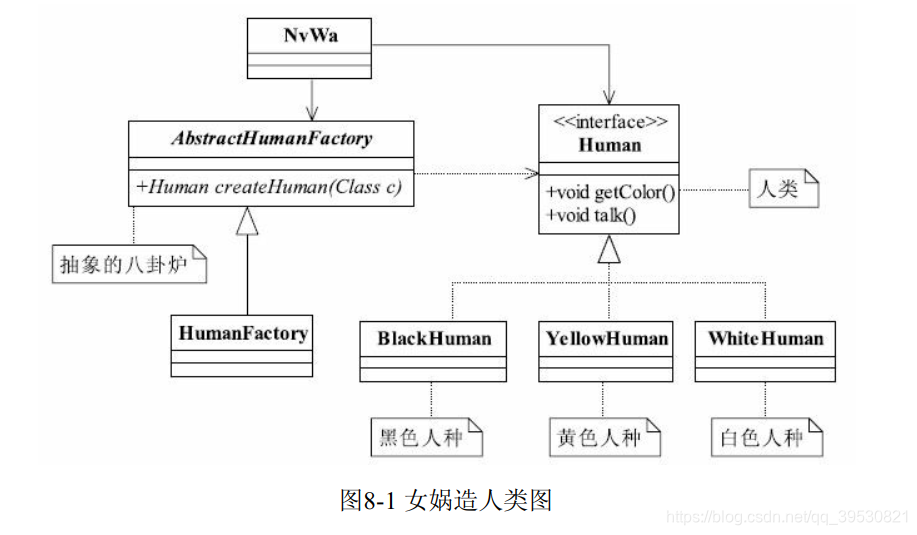
public interface Human { void getColor(); void talk();} 各个人种:
public class YellowHuman implements Human { @Override public void getColor() { System.out.println("YellowHuman is yellow"); } @Override public void talk() { System.out.println("YellowHuman talk"); }}public class WhiteHuman implements Human { @Override public void getColor() { System.out.println("WhiteHuman is white"); } @Override public void talk() { System.out.println("WhiteHuman talk"); }}public class BlackHuman implements Human { @Override public void getColor() { System.out.println("BlackHuman is black"); } @Override public void talk() { System.out.println("BlackHuman talk"); }} 工厂:
public abstract class AbstractHumanFactory { public abstract T createHuman(Class c);}public class HumanFactory extends AbstractHumanFactory { @Override public T createHuman(Class c) { T instance = null; try { instance = (T) Class.forName(c.getName()).newInstance(); } catch (Exception e) { System.out.println("创建人类失败"); } return instance; }} 女娲造人:
public class NvWa { public static void main(String[] args) { HumanFactory humanFactory = new HumanFactory(); YellowHuman yellowHuman = humanFactory.createHuman(YellowHuman.class); WhiteHuman whiteHuman = humanFactory.createHuman(WhiteHuman.class); BlackHuman blackHuman = humanFactory.createHuman(BlackHuman.class); yellowHuman.getColor(); yellowHuman.talk(); whiteHuman.getColor(); whiteHuman.talk(); blackHuman.getColor(); blackHuman.talk(); }} 2. 定义和特点
定义一个创建对象的接口,让子类决定实例化哪个类。工厂方法使得类的实例化延迟到子类。
有以下特点:
- 良好的封装性,代码结构清晰,调用者只需知道产品的类名或其他字符串就可以创建产品对象,不需要了解产品的创建过程;
- 扩展性优秀,可以扩展产品,像上面就可以增加棕色人种;
符合以下三个原则;
- 迪米特原则,工厂模式不需要对产品了解;
- 依赖倒置原则,只依赖产品的接口或者抽象类;
- 里氏替换原则,创建产品的方法参数是接口或抽象类。
3. 工厂模式的扩展
3.1 简单工厂模式
也叫静态工厂模式。
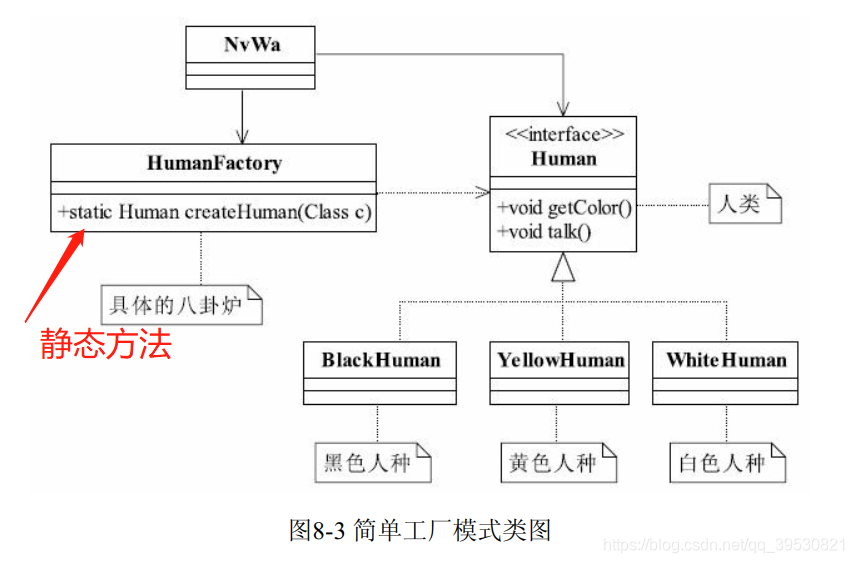
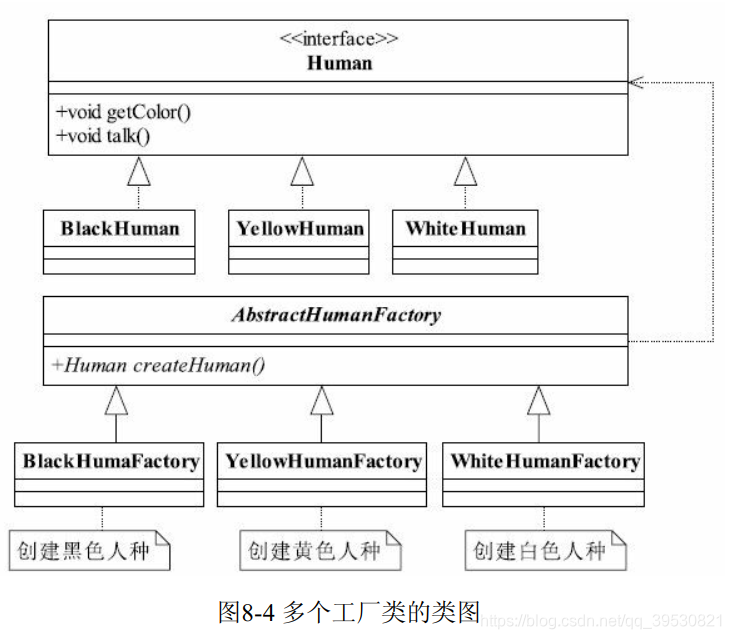
3.2 升级为多个工厂模式
转载地址:http://xphwz.baihongyu.com/
你可能感兴趣的文章